3He(e,e'd) Asymmetries
Consistency checks:
I have three sets of data, taken at different Q**2 and different \theta_{pq}.
This week I was trying various cuts to check if the data are consistent. I performed
various \theta_{pq} and \phi_{pq} cuts to get BB=82deg results from BB=75deg results.
These cuts still cause me some problems. Later I also applied various Q**2 cuts
to come from HRSL=12.5deg data to HRSL=14.5deg data. This seems to be working
well. I used longitudinal data (best statistics), to perform these checks:
\theta_{pq} and \phi_{pq} cuts:
BB=75deg data:
01.)  02.)
02.)  03.)
03.) 
BB=82deg data:
04.)  05.)
05.)  06.)
06.) 
Comparison:
07.)  08.)
08.) 
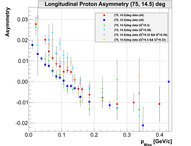
Q**2 cuts
09.) 
10.) 
Q**2 <0.3 (GeV/c)**2:
11.)  12.)
12.) 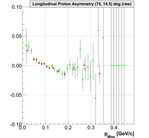 13.)
13.)  14.)
14.) 
0.3 < Q**2 <0.33 (GeV/c)**2:
15.)  16.)
16.)  17.)
17.)  18.)
18.) 
0.33 < Q**2 <0.36 (GeV/c)**2:
19.) 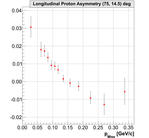 20.)
20.) 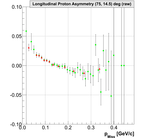 21.)
21.)  22.)
22.) 
Q**2 >0.36 (GeV/c)**2:
23.)  24.)
24.)  25.)
25.)  26.)
26.) 
Elastic Proton asymmetry:
I am trying to get the same value of the proton polarization for both sets of data.
As an additional check I plotted form-factor ratio. I believed that with this
test I could check if the observed discrepancy is a result of beam/target polarization
issues or a results of not properly reconstructed asymmetries. Unfortunately I realized
that the error bars on these ratios are very large. Because of that I can not draw any
serious conclusion from this ratio.
27.) 
I have also been joining data points at low missing momentum (up to 0.1GeV/c), but
results were still not consistent. Only absolute asymmetries were smaller.
I also had some worries, that this is not a legitimate procedure, since the majority of
our data points lie below p_miss < 0.1GeV/c
Next week:
- Analyze the rest of the 12.5 data without compression. This takes a while,
because files are large.
- Make checks (Q**2 cuts etc.) on these data.
- Plot asymmetries as a function of BB momentum
Last modified: 10/12/11
 02.)
02.)  03.)
03.) 
 05.)
05.)  06.)
06.) 
 08.)
08.) 


 12.)
12.)  13.)
13.)  14.)
14.) 
 16.)
16.)  17.)
17.)  18.)
18.) 
 20.)
20.)  21.)
21.)  22.)
22.) 
 24.)
24.)  25.)
25.)  26.)
26.) 
