TgDelta Calibration
I am trying to determine matrix elements for the TgDelta optics variable. With my
new method of solving large over-determined set of linear equations I can use only
data, where momentum of the particle can be directly expressed as a function of the
TgDelta matrix elements. I can use elastic data and precisely chosen sets (punch-through points) of production data. Calibration via missing mass determination, using quasi-elastic data
is with this method not possible, because the equations that we have can not be
linearized. If we would trust the analytic model, we could use those results to find matrix.
I will not determine matrix elements directly from the analytical model, because I would
like to get results with higher precision. However, I have used it (at least for now) to find
relevant matrix elements. At the moment I am also considering only FpTh/FpX dependence
of the TgDelta variable so that I can use elastic data for the calibration, which are
all gathered one one side (L/R) of the focal plane.
Results of the calibration with Analytical model:
1.) 
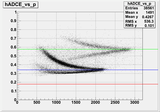
Results of the calibration with the direct fitting of elastic data:
2.) 
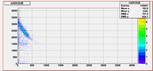
Results of the calibration using Punch-Through points:
3.)  4.)
4.)  5.)
5.) 
6.)  7.)
7.)  8.)
8.) 
Energy-Loss Simulations:
I have used Bethe-Bloch equation to simulate energy-losses of protons and
deuterons. In order to understand particle transport through the BigBite
the simulation results should agree to the measurements to at least some
degree.
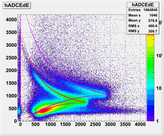
Results of Simulation when only E/dE losses are considered:
Plots show q-vector vs. energy-losses in E-plane for deuterium
elastic runs #3151 and #3608. Quasi-elastic protons were cut away.
9.)  10.)
10.) 
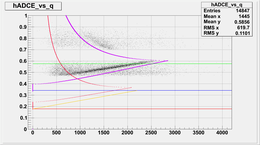
Results of Simulation when transport losses are also considered:
11.)  12.)
12.) 
Results with corrected transport losses:
13.) 
Last modified: 11/17/10


 4.)
4.)  5.)
5.) 
 7.)
7.)  8.)
8.) 
 10.)
10.) 
 12.)
12.) 
