BigBite Optics #9
This week I continued my work on TgPh matrix elements determination. I am still using
Matlab for numerical chi2 minimization of my matrix and it seems it is working well. In order
to find sieve-holes on the top of the sieve-plate, I introduced 18 new higher order terms, which
should solve my problems. I have also changed the way of determining which events in
the focal plane correspond to which hole in the sieve. I discovered ("finally") that this can be
clearly seen from the plots in the focal plane. This approach has an additional advantage, that
it also tells me, which holes are really visible and which are not. This way I did not miss-map
holes any more. Up until now this was a real problem, because I did not know precisely to which
hole (ie. left or right hole if events are in the middle) correspond particular events and wrong
choice had dramatic effects on my matrix. I believe that this problem is solved now.
With these higher order terms I am now able to see all the holes on the top of the sieve. However,
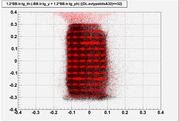
unfortunately these higher order terms introduce oscillations on the edges of the acceptance and this
is not acceptable. This problem still needs to be solved.
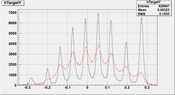
I have also started working in the TgY matrix elements. I already have reasonable approximation for it,
but would still like to get better resolution in TgY (at least for factor 2).
Matrix elements "[TgPh|FpPh]" and "[TgTh|***]"
Matlab Calibration & new Matrix:
[matrix]
t 1 0 0 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
y 1 0 0 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
p 1 0 0 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 0 0 0 -0.0062343 -0.9545440 1.13910000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 1 0 0 3.39098000 -7.6819500 7.76604000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 2 0 0 11.7304000 -19.230500 21.1691000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 3 0 0 14.3041000 -8.6769400 3.53875000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
T 0 0 0 -0.013657 -0.51363 0.058716 0.059744 -0.059852
T 1 0 0 0.45305 0.023602 -0.15936 0.084532 0.0
T 2 0 0 -0.016576 0.12177 -0.016977 0.0 0.0
T 3 0 0 -0.018396 -0.065876 0.0 0.0 0.0
T 4 0 0 0.063481 0.0 0.0 0.0 0.0
T 0 1 0 0.0018086 0.027319 0.021888 0.067522 0.0
T 0 2 0 -0.038123 0.023323 0.53049 0 0.0
T 0 3 0 0.045988 -0.10698 0.0 0 0
T 0 4 0 -0.064298 0 0 0 0
T 0 0 1 -0.0074584 -0.093952 -0.016637 -0.027579 0.0
T 0 0 2 0.14881 0.30279 -0.64125 0.0 0.0
T 0 0 3 -0.18883 2.727 0.0 0.0 0.0
T 0 0 4 -0.15256 0.0 0.0 0.0 0.0
T 0 1 1 -0.10201 -0.40498 -0.028072 0.0 0.0
T 0 2 1 0.11611 -0.52558 0.0 0.0 0.0
T 0 3 1 -1.0489 0.0 0.0 0.0 0.0
T 0 1 2 0.0081171 -0.49757 0.0 0.0 0.0
T 0 2 2 1.3538 0.0 0.0 0.0 0.0
T 0 1 3 -0.078287 0.0 0.0 0.0 0.0
T 1 0 1 0.062559 0.19332 0.089416 0.0 0.0
T 2 0 1 -0.18283 0.33515 0.0 0.0 0.0
T 3 0 1 -0.25355 0.0 0.0 0.0 0.0
T 1 0 2 -0.53321 0.18428 0.0 0.0 0.0
T 2 0 2 0.67786 0.0 0.0 0.0 0.0
T 1 0 3 -2.7152 0.0 0.0 0.0 0.0
T 1 1 0 -0.0092399 -0.12064 0.052921 0.0 0.0
T 2 1 0 0.13073 -0.62477 0.0 0.0 0.0
T 3 1 0 0.46124 0.0 0.0 0.0 0.0
T 1 2 0 -0.013574 -0.73554 0.0 0.0 0.0
T 2 2 0 0.54637 0.0 0.0 0.0 0.0
T 1 3 0 -1.4077 0.0 0.0 0.0 0.0
T 1 1 1 0.81748 -0.075751 0.0 0.0 0.0
T 1 1 2 -2.1847 0.0 0.0 0.0 0.0
T 2 1 1 0.097293 0.0 0.0 0.0 0.0
T 1 2 1 5.1688 0.0 0.0 0.0 0.0
P 0 0 0 -0.0065469 0.0066656 0.033926 -0.060235 -0.11028 0.0
P 1 0 0 -0.003287 -0.04428 0.17645 0.18124 0.0 0.0
P 2 0 0 0.014925 -0.16233 0.2011 0.0 0.0 0.0
P 3 0 0 -0.0068738 -0.46464 0.0 0.0 0.0 0.0
P 4 0 0 0.086207 0 0 0 0 0
P 0 1 0 -0.01136 0.074593 0.3233 -2.9343 0 0
P 0 2 0 -1.1634 1.4897 -2.4912 0 0 0
P 0 3 0 -9.5849 18.437 0 0 0 0
P 0 4 0 -23.478 0 0 0 0 0
P 0 0 1 0.99402 -0.37816 -0.71308 2.1891 6.4929 4.365
P 0 0 2 -1.973 1.6006 -6.0069 0 0 0
P 0 0 3 17.232 -16.699 -0.18624 -1.8665e-05 0 0
P 0 0 4 90.148 0 0 0 0 0
P 0 1 1 3.0823 -3.0949 7.1605 0 0 0
P 0 2 1 37.871 -49.863 0 0 0 0
P 0 3 1 101.83 0 0 0 0 0
P 0 1 2 -48.23 52.383 0 0 0 0
P 0 2 2 -101.7 0 0 0 0 0
P 0 1 3 -61.46 0 0 0 0 0
P 1 0 1 0.0094872 0.55837 -7.2259 -15.508 -9.4952 0
P 2 0 1 -0.17051 7.7126 3.4975 -0.33172 0 0
P 3 0 1 -0.061546 10.05 6.1581 0 0 0
P 1 0 2 2.236 7.3906 0 0 0 0
P 2 0 2 -0.17671 0 0 0 0 0
P 1 0 3 -5.6236 1.6707 -18.479 0 0 0
P 1 1 0 0.2337 -0.82046 5.7896 0 0 0
P 2 1 0 1.0901 -2.9868 0 0 0 0
P 3 1 0 0.14403 0 0 0 0 0
P 1 2 0 0.032203 0.74589 0 0 0 0
P 2 2 0 6.3395 0 0 0 0 0
P 1 3 0 -13.82 0 0 0 0 0
P 1 1 1 -1.7242 -4.8349 0 0 0 0
P 1 1 2 6.3679 0 0 0 0 0
P 2 1 1 -10.647 0 0 0 0 0
P 1 2 1 14.626 0 0 0 0 0
P 4 0 1 -1.858 -0.28142 0 0 0 0
P 5 0 1 -0.57526 0 0 0 0 0
P 2 0 3 32.2 -0.43315 0 0 0 0
P 3 0 3 -19.505 0 0 0 0 0
Y 0 0 0 -0.0321556 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 1 0 -1.0241000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 2 0 -0.4919260 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 0 1 2.8077500 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 1 1 0.72023300 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 2 1 -0.7153320 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
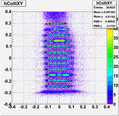
Old approach of sieve-hole search:
1.) 
New approach of sieve-hole search:































































Problems with the last line:
The holes in the most bottom line are still not visible. If I plot each hole separately, I can see,
that holes are there, but they are too wide. Their width is more than twice as normal which consequently
results in a line, when I plot all the holes together.










Fourth-order matrix:
2.)  3.)
3.) 
Matrix with higher order terms:
4.)  5.)
5.) 
Problems with new matrix:
6.) 
7.)  8.)
8.)  9.)
9.) 
ThY matrix elements determination:
10.) 








Last modified: 04/14/10










































































 3.)
3.) 
 5.)
5.) 

 8.)
8.)  9.)
9.) 








