BigBite Optics #6
Matrix elements "[TgPh|FpPh]" and "[TgTh|x]"
I am still working on the matrix elements for TgPh and TgTh. I am working on my
second iteration. I have used my best guess from last week, put it into the BB
matrix and re-done the whole procedure. Now I can see more holes and each hole
contains more events than before. This gives us opportunity to find better matrix
elements.

















































Current results:
My next good optics matrix has the following form:
[matrix]
t 1 0 0 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
y 1 0 0 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
p 1 0 0 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 0 0 0 -0.0062343 -0.9545440 1.13910000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 1 0 0 3.39098000 -7.6819500 7.76604000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 2 0 0 11.7304000 -19.230500 21.1691000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
D 3 0 0 14.3041000 -8.6769400 3.53875000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
T 0 0 0 -0.0144845 -0.5110110 0.0614577 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
T 1 0 0 0.45228300 0.00349067 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 0 0 0 -0.0085540 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 0 0 1 0.99276700 0.19470400 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 0 1 0 0.00000000 -0.1967680 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 0 0 2 0.05101200 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 0 1 1 -0.0299057 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 0 2 0 -0.0249150 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 1 0 1 -0.2368120 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
P 1 1 0 0.22234200 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 0 0 -0.0321556 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 1 0 -1.0241000 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 2 0 -0.4919260 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 0 1 2.8077500 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 1 1 0.72023300 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
Y 0 2 1 -0.7153320 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
1.) 
Next iteration:
2.) 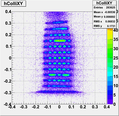 3.)
3.) 
However, I am still using Mathematica to calculate matrix elements. Unfortunately, now that
I have more points and more matrix elements in my procedure, Mathematica fails to find
a fit. It seems that minimization procedure that Mathematica uses requires more memory than
I have in my computer. Therefore it crashes somewhere in the middle of the procedure.
Please see figure below:
4.)  5.)
5.) 
This is a clear sign that Mathematica is not a good choice. Since I am trying
to avoid coding the whole fitting method from scratch, my next step will be to
use Matlab as next choice to do my fitting procedure.
Last modified: 03/17/10


















































 3.)
3.) 
 5.)
5.) 